September 8, 2013

Basic pathfinding

by Alexander Vershilov

Keywords: haskell

In this post I’ll review basic approach to pathfinding using functional approach. It possible that this post doesn’t contain the best approach and all other solutions are welcome.

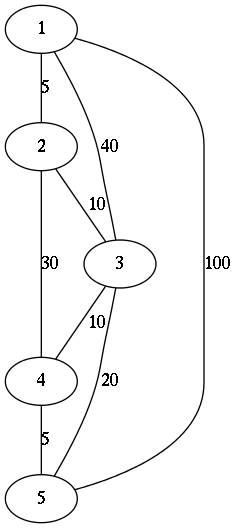
On the right you can see example of a simple map.

Here is a list of imports. I need it because this is pure lhs file that can be downloaded and executed in ghci, so you can skip it.

import           Data.List
import           Data.Monoid
import           Data.Map (Map)
import qualified Data.Map as Map
import           Data.Set (Set)
import qualified Data.Set as Set
import           Data.Function

We will solve simple task of finding the shortest path from one location to another (from 5 to 1). As a first step lets introduce some basic types. Most of them are just type synonyms:

type Loc     = Int                      -- Location
type Dist    = Int                      -- Distance
type History = [Loc]                    -- History
type LMap    = Map Loc [(Loc,Dist)]     -- map
-- here is example of the map
testMap :: LMap
testMap = Map.fromList [(1,[(2,5),(3,40),(5,100)])
                       ,(2,[(1,5),(3,10),(4,30)])
                       ,(3,[(1,40),(2,10),(5,20),(4,10)])
                       ,(4,[(2,30),(3,10),(5,5)])
                       ,(5,[(1,100),(3,20),(4,5)])
                       ]

## Basic algorithm

The basic idea of our solution is: ‘we need to create a list of the locations that is reachable from initial location sorted by distance’. You can this about this solution like we move in all possible directions at the same time. Then we can filter out final destination and find history related to the correct solution.

Terms: frontier - a list of possible locations with distance from the starting point, sorted by ascending distance.

type Frontier0 = [(Loc, Dist)]

So algorithm of generating result list will look like:

0. Add starting point with zero distance to the frontier.
1. Take the first location from the frontier. It will be our next current location.
2. p1 <- get list of the locations reachable from the current location in one step.
3. p2 <- sum distance to the current distance with the distance from the current location to each possible location from p1. Now we have a list of possible locations with distances from the starting point.
4. Add list of the new possible locations (p2) to the frontier.
5. goto 1.

This algorithm will create a list of the possible destinations from the current point. The key of the algorithm is that frontier should be sorted by distance, so every time we will take closest position. It will guarantee that our algorithm will not diverge.

As you’ll see the solution will be a direct translation of literal description to the code. And that is a very nice property of haskell.

Here are few images describing process:

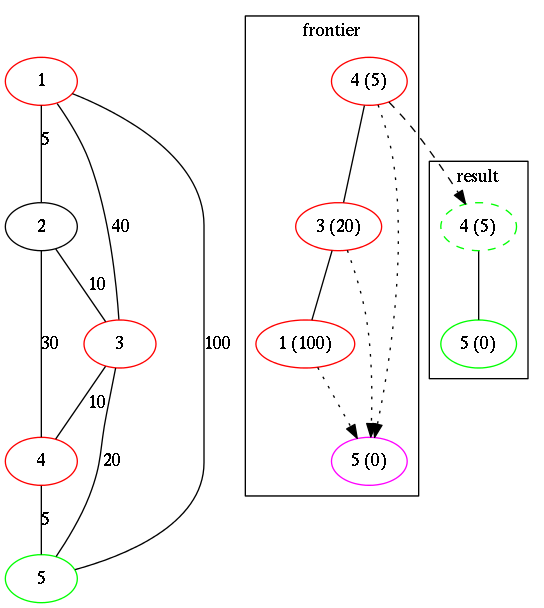
Here is an image of the current state after step 0.

We added 5 to the frontier and then take it as a current location.

Now we have 3 new locations reachable: 1, 3 and 4 (marked with red).

And 4 with distance 5 will be moved to the result list (dashed).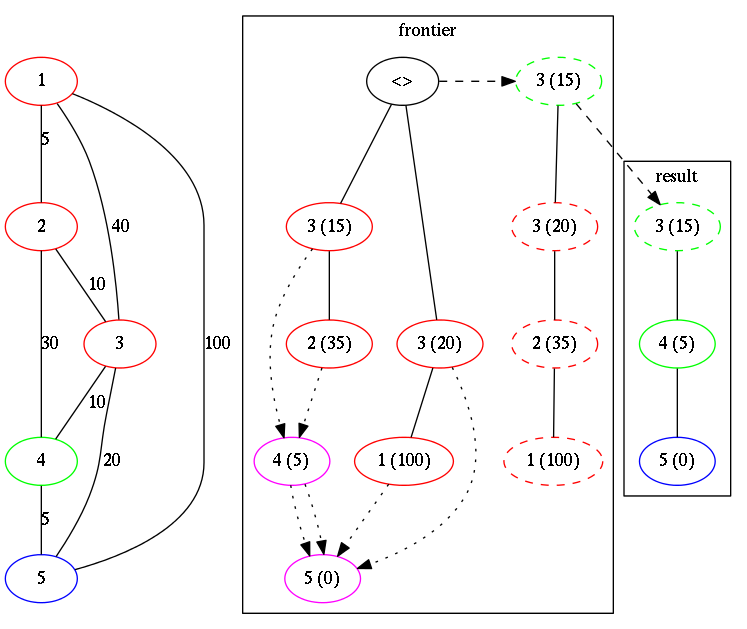

Here is next step.

We took 4 as a new current element.

We found 2 new reachabe locations: 2 and 3.

We added current distance (5) to distances to the current locations and add them to the frontier.

<> is a function that will merge and sort 2 lists. You can see result of the merge shown with dashed lines.

## Additional types.

Now we can review types that we will use.

### Candidate

All elements in a resulting set and a frontier are possible canditas for a solution, so they need to contain all temporary information (Distance) and information that we will need when we’ll filter out this solution (History). So we need to introduce a newtype for a candate, we use newtype here because we will need to redefine some properties otherwise we could use a tuple (,,):

newtype Candidate = Candidate (Loc,Dist,History) deriving Eq   -- possible solution

And helper functions:

candidateLoc :: Candidate -> Loc
candidateLoc (Candidate (x,_,_)) = x

candidateHist :: Candidate -> History
candidateHist (Candidate (_,_,x)) = x

### Ascending list

As we have seen in the algorithm resulting list and frontier are ascending lists. So we may introduce special type that will preserve this property. This will help us to avoid additional mistakes, and can help with undestanding of our solution. This type is isomorphic to the List, however we can’t just use a newtype as we shouldn’t unpack pure list from the AscList:

data AscList a = (:<) a (AscList a) | Nil

It’s easy to see that AscList forms a monoid with regard to concat operation, so we can use this information:

instance Ord a => Monoid (AscList a) where
  mempty = Nil
  mappend Nil b = b
  mappend a Nil = a
  mappend a'@(a :< as) b'@(b :< bs)
     | a < b = a :< (as <> b')
     | otherwise = b :< (a' <> bs)

Introduce two helper functions:

-- | create ascending list from arbitrary list
fromList :: (Ord a) => [a] -> AscList a
fromList = mconcat . map singleton 

-- | convert value to Ascending List
singleton :: a -> AscList a
singleton x = x :< Nil

In order to use Candidates in an AscList we need to introduce ordering on the Candidates:

instance Ord Candidate where
    compare (Candidate (_,d1,_)) (Candidate (_,d2,_)) = compare d1 d2

Now we can guarantee that lists are properly ordered.

### Builder seed.

In order to create list we will use unfoldr :: (b -> Maybe (a, b)) -> b -> [a] combinator. On each step we will create one new element and return new seed. So we will need to store frontier in the seed. Additionaly we will use one optimization: we will store a list of visited locations (that exists in result array) and we will filter out locations that we have visited, so we need to store a set of location. So resulting type will look like:

type Visited = Set Loc                  -- visited locations
type Seed = (AscList Candidate,Visited) -- seed of the algorithm

## Solver

Now we are ready to introduce our solver:

solve :: LMap       -- ^ map
      -> Loc        -- ^ finish location
      -> Loc        -- ^ start location
      -> History
solve mp finish = reverse
                . (finish:)     -- we need to add finish place to the list
                . candidateHist -- we are interested in history only
                . head          -- we need only first solution
                . filter ((==finish) . candidateLoc)  -- take last result
                . unfoldr go    -- generate list of candidates using frontier
                . initial       -- initialize frontier using starting point
 where
    initial i = (singleton $ Candidate (i,0,[]),Set.empty)

In go we need to guarantee that current seed in greater (using Candidate’s ordering) that any other element in list. We can guarantee it because:

0. when we have no elements in list we use first candidate with zero distance
1. all elements in frontier has length > than current location. because we use AscList.
2. all possible locations from current location > than current location as their distance is (current location distance + x, where x ≥ 0).

    go :: Seed -> Maybe (Candidate,Seed)
    go (Nil,_) = Nothing
    go ((Candidate (x,d,h) :< xs),visited) =
       case Map.lookup x mp of  -- read possible locations from map
         Nothing -> go (xs,visited)       -- if thre is no destinaction proceed with next element
         Just ls -> let ls'   = fromList  -- generate AscList from current position
                              . map (\(yl,yd) -> Candidate (yl,yd+d,x:h))  -- increment distance (see 2.)
                              . filter ((`Set.notMember` visited) . fst) $ ls -- remove elements that we have visited
                    in Just ( Candidate (x,d,h)
                              , (ls' <> xs, Set.insert x visited))

Yachoo! we have a solver. However it will work badly on the big maps and we need to use more advanced methods, like A*. But we need to fix Candidate ordering function.

I’ve heard that it is possible to use comonad approach to solve this problem however I couldn’t find any example of this approach.

test = solve testMap 5 1

as a result we will have [5,4,3,2,1]. That is correct solution.